Что такое гравитация для чайников: определение и теория простыми словами

В чём измеряется гравитационная постоянная

Несмотря на то, что гравитационная постоянная численно равна силе, её единицы измерения не ньютоны. Размерность коэффициента может показаться страшной –

Согласно Международной системе единиц (системе интернациональной или СИ), сила измеряется в ньютонах, причём

то есть 1 ньютон – сила, изменяющая скорость килограммового объекта на 1 м/с за одну секунду.

После открытия закона тяготения определено: пара килограммовых тел притягивается друг к другу силой со значением, зависящим обратно пропорционально от квадрата расстояния между объектами.

То есть единица измерения гравитационной силы –

и размерность не совпадает с привычной

Проведём математические вычисления самостоятельно.

Нужно уравнять

Для этого

2 3

Получилась требуемая размерность.

Следовательно, постоянная имеет размерность

Сила притяжения и Писание

Два места из Библии могут помочь нам понять природу гравитации и физическую науку в целом. Первое место, Колоссянам 1:17, объясняет, что Христос «есть прежде всего, и все Им стоит». Греческий глагол стоит (συνισταω sunistao) означает: сцепляться, сохраняться или удерживаться вместе. Греческое использование этого слова за пределами Библии обозначает сосуд, с содержащейся в нем водой. Слово, которое используется в книге Колоссянам, стоит в совершенном времени, что как правило, указывает на настоящее продолжающееся состояние, которое возникло из завершенного прошедшего действия. Один из используемых физических механизмов, о котором идет речь, явно сила притяжения, установленная Творцом и безошибочно поддерживаемая и сегодня. Только представьте: если бы на мгновение перестала действовать сила притяжения, несомненно, наступил бы хаос. Все небесные тела, включая землю, луну и звезды, не удерживались бы больше вместе. Все тот час разделилось бы на отдельные, маленькие части.

Второе место Писания, Евреям 1:3, заявляет, что Христос «держит все словом силы Своей». Слово держит (φερω pherō) снова описывает поддерживание или сохранение всего, включая гравитацию. Слово держит, используемое в этом стихе, означает намного больше, чем просто удерживание веса. Оно включает контроль над всеми происходящими движениями и изменениями внутри вселенной. Это бесконечное задание выполняется через всемогущее Слово Господа, посредством которого начала существовать сама вселенная. Гравитация, «таинственная сила», которая и через четыреста лет исследований остается плохо изученной, является одним из проявлений этой потрясающей божественной заботы о вселенной.

Отношение к универсальному закону

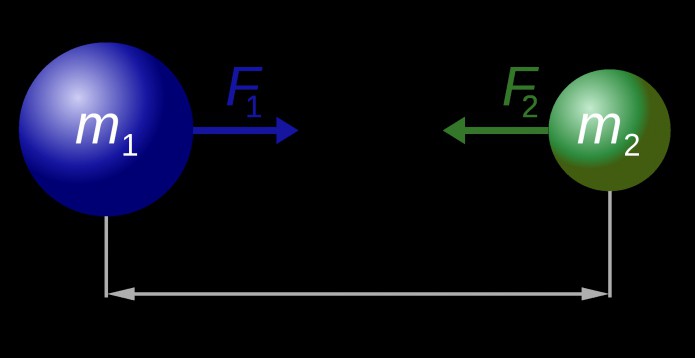
Закон всемирного тяготения Ньютона утверждает, что между любыми двумя массами существует гравитационная сила, равная по величине для каждой массы и выровненная так, чтобы притягивать две массы друг к другу. Формула:

Fзнак равнограммм1м2р2 {\ Displaystyle F = G {\ гидроразрыва {m_ {1} m_ {2}} {r ^ {2}}} \}

где и — любые две массы, — гравитационная постоянная и — расстояние между двумя точечными массами.
м1{\ displaystyle m_ {1}}м2{\ displaystyle m_ {2}}грамм{\ displaystyle G}р{\ displaystyle r}

Два тела вращаются вокруг своего центра масс (красный крест)

Используя интегральную форму закона Гаусса , эту формулу можно распространить на любую пару объектов, один из которых намного массивнее другого — например, планета относительно любого артефакта человеческого масштаба. Расстояния между планетами и между планетами и Солнцем (на много порядков) больше, чем размеры Солнца и планет. Вследствие этого и Солнце, и планеты можно рассматривать как точечные массы, и одна и та же формула применяется к движению планет. (Поскольку планеты и естественные спутники образуют пары сравнимой массы, расстояние r измеряется от общих центров масс каждой пары, а не от прямого общего расстояния между центрами планет.)

Если одна масса намного больше другой, удобно принять ее за эталон для наблюдений и определить ее как источник гравитационного поля, величина и ориентация которого задаются формулой:

граммзнак равно-граммMр2р^{\ displaystyle \ mathbf {g} = — {GM \ over r ^ {2}} \ mathbf {\ hat {r}}}

где — масса источника поля (большего размера), а — единичный вектор, направленный от источника поля к массе образца (меньшей). Отрицательный знак означает, что сила притягивает (указывает назад, к источнику).
M{\ displaystyle M}р^{\ displaystyle \ mathbf {\ hat {r}}}

Тогда вектор силы притяжения на массу образца можно выразить как:
F{\ displaystyle \ mathbf {F}}м{\ displaystyle m}

Fзнак равномграмм{\ Displaystyle \ mathbf {F} = м \ mathbf {g}}

Вот это трения , ускорение свободного падение поддерживается массами выборки под притяжением гравитационного источника. Это вектор, ориентированный к источнику поля, величина которого измеряется в единицах ускорения. Вектор ускорения свободного падения зависит только от того, насколько массивен источник поля и от расстояния r до массы образца . Это не зависит от величины малой массы образца.
грамм{\ displaystyle \ mathbf {g}}м{\ displaystyle m}M{\ displaystyle M}м{\ displaystyle m}

Эта модель представляет собой гравитационное ускорение «дальнего поля», связанное с массивным телом. Когда размеры тела нетривиальны по сравнению с интересующими расстояниями, принцип суперпозиции может быть использован для дифференциальных масс для предполагаемого распределения плотности по всему телу, чтобы получить более подробную модель гравитационного поля «ближнего поля». ускорение. Для спутников, находящихся на орбите, модели дальнего поля достаточно для грубых расчетов зависимости высоты от периода , но не для точной оценки будущего местоположения после нескольких орбит.

Более подробные модели включают (среди прочего) выпуклость на экваторе Земли и нерегулярные концентрации массы (из-за ударов метеоров) Луны. Миссия Gravity Recovery and Climate Experiment (GRACE), запущенная в 2002 году, состоит из двух зондов, получивших прозвище «Том» и «Джерри», которые находятся на полярной орбите вокруг Земли и измеряют разницу в расстояниях между двумя зондами, чтобы более точно определить гравитационное давление. поле вокруг Земли и отслеживать изменения, происходящие с течением времени. Точно так же миссия Лаборатории восстановления силы тяжести и внутренней обстановки в 2011-2012 годах состояла из двух зондов («Отлив» и «Поток») на полярной орбите вокруг Луны для более точного определения гравитационного поля для будущих навигационных целей и для получения информации о Внешний вид Луны.

Гравитационное притяжение

Закон всемирного тяготения.

В рамках классической механики гравитационное притяжение описывается законом всемирного тяготения Ньютона, который гласит, что сила гравитационного притяжения между двумя материальными точками массы и , разделёнными расстоянием , пропорциональна обеим массам и обратно пропорциональна квадрату расстояния — то есть:

−11

Закон всемирного тяготения — одно из приложений закона обратных квадратов, встречающегося также и при изучении излучений, и являющегося прямым следствием квадратичного увеличения площади сферы при увеличении радиуса, что приводит к квадратичному же уменьшению вклада любой единичной площади в площадь всей сферы.

Гравитационное поле, так же как и поле силы тяжести, потенциально. Это значит, что можно ввести потенциальную энергию гравитационного притяжения пары тел, и эта энергия не изменится после перемещения тел по замкнутому контуру. Потенциальность гравитационного поля влечёт за собой закон сохранения суммы кинетической и потенциальной энергии и при изучении движения тел в гравитационном поле часто существенно упрощает решение. В рамках ньютоновской механики гравитационное взаимодействие является дальнодействующим. Это означает, что как бы массивное тело ни двигалось, в любой точке пространства гравитационный потенциал зависит только от положения тела в данный момент времени.

Большие космические объекты — планеты, звезды и галактики имеют огромную массу и, следовательно, создают значительные гравитационные поля.

Гравитация — слабейшее взаимодействие. Однако, поскольку оно действует на любых расстояниях, и все массы положительны, это, тем не менее, очень важная сила во Вселенной. В частности, электромагнитное взаимодействие между телами в космических масштабах мало, поскольку полный электрический заряд этих тел равен нулю (вещество в целом электрически нейтрально).

Также гравитация, в отличие от других взаимодействий, универсальна в действии на всю материю и энергию. Не обнаружены объекты, у которых вообще отсутствовало бы гравитационное взаимодействие.

Из-за глобального характера гравитация ответственна и за такие крупномасштабные эффекты, как структура галактик, черные дыры и расширение Вселенной, и за элементарные астрономические явления — орбиты планет, и за простое притяжение к поверхности Земли и падения тел.

Гравитация была первым взаимодействием, описанным математической теорией. Аристотель (IV в. до н.э.) считал, что объекты с разной массой падают с разной скоростью. Только много позже (1589) Галилео Галилей экспериментально определил, что это не так — если сопротивление воздуха устраняется, все тела ускоряются одинаково. Закон всеобщего тяготения Исаака Ньютона (1687) хорошо описывал общее поведение гравитации. В 1915 году Альберт Эйнштейн создал Общую теорию относительности, более точно описывающую гравитацию в терминах геометрии пространства-времени.

Сила тяжести как частный случай закона всемирного тяготения

Создав математическую модель притяжения, Ньютон установил, что сила тяжести, чьё влияние видел и испытывал на себе каждый, является лишь одним из проявлений всемирного тяготения, которое утверждает, что все тела во Вселенной, включая планеты, звёзды, астероиды и т.д., воздействуют друг на друга с определённой силой.

Чтобы узнать значение этой силы, исходящей от Земли, нужно воспользоваться формулой, выражающей прямо пропорциональную зависимость воздействия и массы объекта:

F_тяж = g∙m,

где g = G∙(m_З / R_З2),

сила тяжести

На поверхности значение ускорения свободного падения принимают равным 9,81 м/с2. Если же тело удалено от поверхности Земли, значение g можно найти по формуле:

g = G∙(m_З / (R_З+h)2),

где h – расстояние до земли.

Таким образом, действие силы тяжести на тело уменьшается с увеличением высоты.

Интересный факт: если принять силу тяжести, действующую на Земле, за единицу, то можно проанализировать значение притяжения на поверхности других небесных тел. Так, самое большое воздествие тяготения испытает на себе тело на поверхности Юпитера – 2,442, а самое маленькое – на Луне (0,165).

Квантовая гравитация

Универсальной квантовой теории, объяснившей бы само понятие гравитации, ещё не разработано. Для представления гравитационного взаимодействия было бы вероятно предложить гравитонный обмен, в котором гравитоны выступают в качестве калибровочных бозонов со спином 2. Но такая теория не считается удовлетворительной. На существующее время есть несколько подходов, разрешающих квантование гравитации. Эти подходы считаются достаточно перспективными.

• Теория струн. Она заменяет частицы фона пространства-времени на струны и браны (подобие струн). Для решения многомерных задач, браны видятся как частицы уже многомерные, но в тоже время они и структуры пространства-времени. Гравитоны здесь становятся состоянием струн, а не отдельными частицами. Хотя низкие энергии их к ним и причисляют.
• Петлевая квантовая гравитация. Здесь время и пространство являются дискретными частями. Они не привязаны к фону пространства-времени, являясь квантовыми пространственными ячейками. Они между собой соединены таким образом, что в малых временных масштабах представляются дискретной структурой пространства. При укрупнении масштабов, части плавно становятся непрерывным пространством-временем. Петлевая гравитация способна описать сущность Большого взрыва, а также пролить свет на его преддверие. Это даже позволяет обходиться без привлечения бозона Хиггса.

Оценка g по закону всемирного тяготения

Из закона всемирного тяготения , сила , действующая на тело воздействует Земли сила тяготения определяется

Fзнак равнограммм1м2р2знак равно(граммм1р2)м2{\ displaystyle F = G \, {\ frac {m_ {1} m_ {2}} {r ^ {2}}} = \ left (G \, {\ frac {m_ {1}} {r ^ {2) }}} \ вправо) м_ {2}}

где r — расстояние между центром Земли и телом (см. ниже), и здесь мы принимаем m ₁ за массу Земли, а m ₂ за массу тела.

Кроме того, второй закон Ньютона , F = ma , где m — масса, а a — ускорение, говорит нам, что

Fзнак равном2грамм{\ Displaystyle F = m_ {2} \, g \,}

Сравнивая две формулы, видно, что:

граммзнак равнограммм1р2{\ displaystyle g = G \, {\ frac {m_ {1}} {r ^ {2}}}}

Так, чтобы найти ускорение силы тяжести на уровне моря, подставить значения из гравитационной постоянной , G , Земли масса (в кг), м ₁ , а Земли радиус (в метрах), г , чтобы получить значение г :

граммзнак равнограммм1р2знак равно6,67408⋅10-11м3⋅kграмм-1⋅s-25,9722⋅1024kграмм(6,371⋅106м)2знак равно9,81998м⋅s-2{\ displaystyle g = G \, {\ frac {m_ {1}} {r ^ {2}}} = 6.67408 \ cdot 10 ^ {- 11} \, \ mathrm {m} ^ {3} \ cdot \ mathrm {kg} ^ {- 1} \ cdot \ mathrm {s} ^ {- 2} \, \, \, {\ frac {5.9722 \ cdot 10 ^ {24} \, \ mathrm {kg}} {\ left ( 6.371 \ cdot 10 ^ {6} \, \ mathrm {m} \ right) ^ {2}}} = 9.81998 \, \, {\ mbox {m}} \ cdot {\ mbox {s}} ^ {- 2 }}

Эта формула работает только из-за того математического факта, что сила тяжести однородного сферического тела, измеренная на его поверхности или над ней, такая же, как если бы вся его масса была сосредоточена в точке в его центре. Это то, что позволяет нам использовать радиус Земли в качестве r .

Полученное значение примерно соответствует измеренному значению g . Разницу можно объяснить несколькими факторами, упомянутыми выше в разделе «Варианты»:

• Земля неоднородна
• Земля не является идеальной сферой, и для ее радиуса необходимо использовать среднее значение.
• Это вычисленное значение g включает только истинную гравитацию. Это не включает уменьшение сдерживающей силы, которое мы воспринимаем как уменьшение силы тяжести из-за вращения Земли, и некоторую часть силы тяжести, противодействующей центробежной силе.

Существуют значительные погрешности в значениях r и m _1, используемых в этом расчете, и значение G также довольно сложно точно измерить.

Если G , g и r известны, то обратный расчет даст оценку массы Земли. Этот метод использовал Генри Кавендиш .

Связанные определения

Пусть μ =м _пм _е знак равно 1 836 0,152 672 47 (80) будут безразмерное отношение протона к электрону масс , отношение массы покоя от протона к томучто из электрона . Другие определения α _G , которые были предложены в литературе, отличаются от приведенного выше только множителем μ или его квадратом;

• Если α _G определяется с использованием массы одного электрона m _e и одного протона ( m _p = μm _e ), то α _G =1,752 × 10 -45 мк =3,217 × 10 −42 иαα _G≈ 10 39 .αα _Gтаким образом определено C у Эддингтона (1935: 232), где постоянная Планка заменяет «приведенную» постоянную Планка;
• (4.5) в работе Барроу и Типлера (1986) неявно определяет αα _G так как e 2Gm _p m _e≈ 10 39 . Хотя они не называютαα _Gопределенная таким образом, она, тем не менее, играет роль в их широком обсуждении астрофизики , космологии , квантовой физики и антропного принципа ;
• N в Rees (2000) — этоαα _G знак равно α1,752 × 10 −45 мкм 2 знак равно α5,906 × 10 -39≈ 10 36 , где знаменатель определяется через пару протонов.

Обсуждение

Существует произвол в выборе массы частицы (в то время как α является функцией элементарного заряда , α G обычно является функцией массы покоя электрона ). В этой статье α G определяется в терминах пары электронов, если не указано иное

И хотя связь между α G и гравитацией в некоторой степени аналогична соотношению постоянной тонкой структуры и электромагнетизма , важное различие состоит в том, что стандартное определение α G описывает отношение только с точки зрения массы электрона, тогда как постоянная тонкой структуры относится к элементарному заряду , который является квантом, не зависящим от выбора частицы.

Электронов является стабильной частицей , обладающей один элементарного заряда и одну массы электрона . Следовательно, отношениеαα _Gизмеряет относительную силу электростатических и гравитационных сил между двумя электронами. Выражаясь в натуральных единицах (так что 4π G = c = ħ = ε = 1 ), константы принимают вид α =e 24πи α _G =м _е 24π, в результате получается значимое соотношение αα _G= (ем _е)2. Таким образом, отношение заряда электрона к его массе (в натуральных единицах ) определяет относительную силу электромагнитного и гравитационного взаимодействия между двумя электронами.

α на 43 порядка больше, чем α _G, рассчитанное для двух электронов (или на 37 порядков для двух протонов). Электростатическая сила между двумя заряженными элементарными частицами , значительно больше , чем соответствующая гравитационная силой между ними. Таким образом, гравитационным притяжением элементарных частиц, заряженных или нет, можно пренебречь. Гравитация доминирует для макроскопических объектов, потому что они электростатически нейтральны в очень высокой степени.

α _G имеет простую физическую интерпретацию: это квадрат массы электрона , измеренный в единицах массы Планка . В силу этого α _G связан с механизмом Хиггса , который определяет массы покоя элементарных частиц . α _G может быть измерен только с относительно низкой точностью и редко упоминается в физической литературе.

Так как

αграммзнак равнограммме2ℏcзнак равно(тпωC)2{\ displaystyle \ alpha _ {\ text {G}} = {\ frac {Gm _ {\ text {e}} ^ {2}} {\ hbar c}} = \ left (t _ {\ text {P}} \ омега _ {\ text {C}} \ right) ^ {2}}

где т _Р является время Планка , α _G связан с Q , _C , то угловая частота комптоновской из электрона .

Сила тяготения

В 1682 году Исаак Ньютон открыл закон всемирного тяготения. Он звучит так: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.

Формула силы тяготения согласно этому закону выглядит так:

Закон всемирного тяготения F = G * (Mm/R2) F — сила тяготения M — масса первого тела (часто планеты) m — масса второго тела R — расстояние между телами G — гравитационная постоянная G = 6,67 × 10-11м3·кг-1·с-2

Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз.

Закон всемирного тяготения используют, чтобы вычислить силы взаимодействия между телами любой формы, если размеры тел значительно меньше расстояния между ними.

Если мы возьмем два шара, то для них можно использовать этот закон вне зависимости от расстояния между ними. За расстояние R между телами в этом случае принимается расстояние между центрами шаров.

Приливы и отливы существуют благодаря закону всемирного тяготения. В этом видео я рассказываю, что общего у приливов и прыщей.

Гравитация от Эйнштейна

Задолго до Ньютона и Эйнштейна о гравитации говорил еще Аристотель. Он выдвинул теорию о том, что скорость падения объекта напрямую зависит от его массы. Но о том, что ускорение свободного падения одинаково для всех, он не знал. Об этом догадался только Галилей.

Далее в Общей теории относительности (ОТО) Эйнштейн более подробно описал гравитацию, связав ее с пространством-временем. Да-да, так как они неразрывны, гравитация искривляет не только материю, но и время. Из-за этого время в космосе идет медленнее.

Гравитация от Эйнштейна

Вы помните, что орехи скатываются к яблокам и все такое, но в таком случае, почему Луна до сих пор не рухнула на Землю? Потому что сила гравитационного взаимодействия крайне слаба, но действует на абсолютно любые расстояния. Она даже имеет четкую формулу для расчета: F_g=G(m₁m₂/r2) – то есть это зависимость масс двух объектов от квадрата расстояния между ними, умноженная на гравитационную постоянную. Эту формулу учат в школьном курсе физики, если что. Из этого следует, что чем больше масса тела, тем большее гравитационное поле оно может создать.

В таком случае, многие могут спросить: «почему Луна не падает на Землю под действием гравитации?». Взгляните на формулу – что такое G? Это гравитационная постоянная, равная 6,67408×10-11 м3кг-1с-2. Даже если все здесь кажется вам лютейшим бредом, то 10-11 более наглядно выглядит так: 0,00000000001. Вы отдаете себе отчет в том, на сколько это мало? Ровно настолько, что даже Луна не падает на Землю, не говоря уже о том, что вы не можете притягивать к себе мелкие предметы силой гравитационного взаимодействия, которым, кстати, тоже обладаете.

Все объекты во Вселенной так или иначе подвержены гравитации. Именно Эйнштейн заговорил об «искривлении» пространства. Он считал, что подобное взаимодействие не результат влияния сил, а изменений в самом пространственно-временном континууме. Как это происходит? Из-за массы и энергии. Думаю, многие из вас уже поняли, к чему я веду. ОТО гласит о том, что масса и энергия едины, и именно из-за их взаимодействия искривляется пространство-время. Все вы хоть раз в жизни слышали об этой формуле: E=mc2 – она объясняет, как, но не говорит почему. Гравитация – очень обширное понятие. Она отвечает и за земное притяжение нас с вами и за расширение самой Вселенной. Поэтому описать все это каким-то единым законом до сих пор ни у кого не получилось.

Применение закона всемирного тяготения

Закон всемирного тяготения – это фундаментальный закон механики, после формулировки которого стало возможно объяснение и предсказание множества природных явлений. К ним относятся:

• приливы и отливы;
• точное время и место лунных и солнечных затмений;
• масса Солнца и других астрономических тел;
• орбиты движения планет и их спутников.

Открытие планет с использованием закона всемирного тяготения

После открытия явления притяжения астрономы и физики могли, опираясь на закон Ньютона и соотношения Кеплера, определять траектории движения наблюдаемых планет Солнечной системы и указывать их координаты в любой момент времени, причём правильность вычислений подтверждалась эмпирически – результатами астрономических наблюдений.

В 1781 году Уильямом Гершелем была открыта седьмая планета Солнечной системы – Уран. Следуя отработанному алгоритму, астроном рассчитал траекторию своего открытия и его орбиту, однако в первой половине XIX века учёные обнаружили несоответствие вычисленных и реальных координат. Возникло предположение, что, помимо Солнца и шести других планет, на Уран воздействует ещё одна планета, находящаяся за ним.

В 1846 году ночью 23 сентября на основании теоретических расчётов, выполненных по имеющимся отклонениям Урана от рассчитанной траектории, молодым сотрудником Британской обсерватории Иоганном Галле была обнаружена предсказанная планета, названная Нептуном.

планета Нептун

Интересный факт: расчёты, после проведения которых стало возможно открытие, в одно и то же время совершили два учёных, независимо друг от друга – Джон Адамс и Урбен Леверье.

Спустя практически 100 лет, 18 февраля 1930 года, подобным образом была открыта девятая планета – Плутон, которая из-за относительно небольших размеров и массы считается карликовой.

Что такое и чему равна гравитационная постоянная

Формула закона всемирного тяготения, известная по курсу школьной механики:

формула закона всемирного тяготения

G – коэффициент пропорциональности или гравитационная постоянная;

m_1, m₂ – массы двух тел, испытывающих взаимное притяжение;

r – расстояние между ними.

Коэффициент пропорциональности G обозначает силу, с которой притягивается пара килограммовых объектов, расположенных друг от друга на метровом расстоянии. Значение константы обычно принимается равным:

значение гравитационной постоянной

Столь маленькое число объясняет, почему несмотря на постоянное действие гравитации люди, находящиеся рядом, не чувствуют силу тяготения – она проявляется на объектах огромных масс, имеющих высокие порядки, например, массе планет, Солнца, других звёзд.

гравитационная постоянная в законе всемирного тяготения

Есть ли в космосе гравитация

Когда мы смотрим кино о космосе или видим трансляцию с МКС, в которой космонавты парят в невесомости, многие из нас думают, что там нет гравитации. Это ошибка.

На самом деле гравитация на орбите не то, что есть, она там почти ничем не отличается от той, что мы ощущаем на Земле. Если брать расстояние от центра Земли до МКС, то оно будет примерно на 10 процентов больше расстояния от центра Земли до ее поверхности. Если вспомнить, что гравитация зависит от размера тел и от их расстояния друг от друга, то становится понятно, что гравитация на орбите сильно меньше земной.

Космонавты могут ощущать невесомость не из-за того, что на орбите нет гравитации, а из-за того, что они постоянно находятся в состоянии свободного падения вместе со своим кораблем или космической станцией. Тем не менее, если поставить огромную стремянку и подняться на верхнюю ступеньку, которая будет на высоте орбиты МКС, мы не взлетим, а будем стоять на ней. Сила нашего притяжения немного изменится, но не настолько, чтобы взлететь.

Это не из-за отсутствия гравитации, а наоборот, из-за того, что она есть.

Если говорить совсем просто, космическая станция на орбите движется с огромной скоростью и постоянно стремится как бы пролететь мимо Земли. Ее гравитация в свою очередь удерживает станцию от ”улета”. В итоге, космонавты с их кораблем крутятся вокруг Земли и за счет центробежной силы находятся в уравновешенном состоянии невесомости. Получается, что гравитация на орбите есть и более того, именно она позволяет космонавтам испытывать невесомость, как бы парадоксально это не прозвучало.

Небесная механика и некоторые её задачи

Раздел механики, изучающий движение тел в пустом пространстве только под действием гравитации, называется небесной механикой.

Наиболее простой задачей небесной механики является гравитационное взаимодействие двух точечных или сферических тел в пустом пространстве. Эта задача в рамках классической механики решается аналитически в замкнутой форме; результат её решения часто формулируют в виде трёх законов Кеплера.

При увеличении количества взаимодействующих тел задача резко усложняется. Так, уже знаменитая задача трёх тел (то есть движение трёх тел с ненулевыми массами) не может быть решена аналитически в общем виде. При численном же решении достаточно быстро наступает неустойчивость решений относительно начальных условий. В применении к Солнечной системе эта неустойчивость не позволяет предсказать точно движение планет на масштабах, превышающих сотню миллионов лет.

В некоторых частных случаях удаётся найти приближённое решение. Наиболее важным является случай, когда масса одного тела существенно больше массы других тел (примеры: Солнечная система и динамика колец Сатурна). В этом случае в первом приближении можно считать, что лёгкие тела не взаимодействуют друг с другом и движутся по кеплеровым траекториям вокруг массивного тела. Взаимодействия же между ними можно учитывать в рамках теории возмущений и усреднять по времени. При этом могут возникать нетривиальные явления, такие как резонансы, аттракторы, хаотичность и т. д. Наглядный пример таких явлений — сложная структура колец Сатурна.

Несмотря на попытки точно описать поведение системы из большого числа притягивающихся тел примерно одинаковой массы, сделать этого не удаётся из-за явления динамического хаоса.

Примечания[править | править код]

1. Вайнберг С. Первые три минуты. — М.: Энергоиздат, 1981. — С. 135.
2. Нарликар Дж. Неистовая вселенная. — М.: Мир, 1985. — С. 25. — Тираж 100 000 экз.
3. Нарликар Дж. Гравитация без формул. — М.: Мир, 1985. — С. 144. — Тираж 50 000 экз.
4. Сивухин Д. В. Общий курс физики. Механика. — М., Наука, 1979. — Тираж 50 000 экз. — с. 311.
5. В. Паули Нарушение зеркальной симметрии в законах атомной физики // Теоретическая физика 20 века. Памяти Вольфганга Паули. — М., ИЛ, 1962. — c. 383
6. G. Rosi, F. Sorrentino, L. Cacciapuoti, M. Prevedelli, G. M. Tino. . Nature (18 июня 2014).
7. Нарликар Дж. Неистовая вселенная. — М.: Мир, 1985. — С. 70. — Тираж 100 000 экз.
8. Нарликар Дж. Гравитация без формул. — М.: Мир, 1985. — С. 87. — Тираж 50 000 экз.
9. См. аналогию между слабым гравитационным полем и электромагнитным полем в статье гравитомагнетизм.
10. Канонической эта теория является в том смысле, что она наиболее хорошо разработана и широко используется в современной небесной механике, астрофизике и космологии, причём количество надёжно установленных противоречащих ей экспериментальных результатов практически равно нулю.
11. Иваненко Д. Д., Пронин П. И., Сарданашвили Г. А. Калибровочная теория гравитации. — М.: Изд. МГУ, 1985.
12. Brans, C. H.; Dicke, R. H. (November 1 1961). «Mach’s Principle and a Relativistic Theory of Gravitation». Physical Review 124 (3): 925—935. DOI:10.1103/PhysRev.124.925. Retrieved on 2006-09-23.
13. С ортодоксальной точки зрения это уравнение представляет собой координатное условие.
14. Яворский Б. М., Детлаф А. А., Лебедев А. К. Справочник по физике для инженеров и студентов вузов. — М.: Оникс, 2007. — С. 948. — ISBN 978-5-488-01248-6 — Тираж 5100 экз.
15. Нарликар Дж. Гравитация без формул. — М.: Мир, 1985. — С. 145. — Тираж 50 000 экз.
16. Вайнберг С. Первые три минуты. — М.: Энергоиздат, 1981. — С. 136.

Гравитационные силы: определение

Первая количественная теория гравитации, основанная на наблюдениях движения планет, была сформулирована Исааком Ньютоном в 1687 году в его знаменитых «Началах натуральной философии». Он писал, что силы притяжения, которые действуют на Солнце и планеты, зависят от количества вещества, которое они содержат. Они распространяются на большие расстояния и всегда уменьшаются как величины, обратные квадрату расстояния. Как же можно вычислить эти гравитационные силы? Формула для силы F между двумя объектами с массами m₁ и m₂, находящимися на расстоянии r, такова:

F=Gm1m2/r2,где G — константа пропорциональности, гравитационная постоянная.

Что такое гравитация простыми словами детям.

с лат. gravitas — «тяжесть» ) — невидимая сила , притягивающая объекты с меньшей массой к более массивным. Таким образом определяющая положение галактик, планет, спутников и всех небесных тел. В контексте Земли отвечает за то, что объекты притягиваются к поверхности и не улетают за пределы планеты. Это одно из четырех фундаментальных взаимодействий в физике, определяющих функционирование вселенной, наряду со слабым и сильным атомными взаимодействиями и электромагнетизмом.

Точного научного определения термина не существует, поскольку подходы к изучению гравитации и теории относительно её природы постоянно разрабатываются, дополняются и совершенствуются. Актуальными на сегодня являются закон всемирного тяготения Ньютона вместе с его дополнениями и общая теория относительности Эйнштейна.

Гравитация и закон всемирного тяготения

Закон всемирного тяготения, предложенный Ньютоном, не ставит своей целью описание природы возникновения гравитации, но позволяет совершать верные математические расчеты на практике. Для этого пользуются формулой

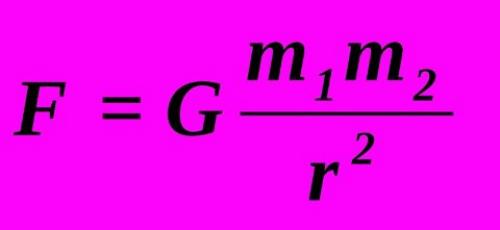
, где:

• F — сила притяжения;
• r — расстояние между их центрами;
• G — гравитационная постоянная, равная 6.67×10 -11 м 3 /кг×с 2 и отражающая то, с какой силой бы действовали друг на друга два тела, размещенные на расстоянии 1 метра и имеющие одинаковую массу в 1 килограмм.

Собственное гравитационное поле создается каждым объектом Вселенной вне зависимости от его массы.

Гравитация на каждой из планет разная и напрямую зависит от массы астрономического тела. Так, к примеру, показатели гравитации на Юпитере многократно превышают земные. На тело, имеющее земной вес в 60 килограмм, Юпитер будет оказывать такую гравитацию, как Земля оказывает на тело с массой 142 килограмма.

Гравитация и общая теория относительности

Несмотря на то, что закон всемирного тяготения Ньютона отлично справляется с математическим описанием гравитации, он порождает конфликты и несоответствия, когда речь заходит о дальности действия и скорости распространения этой величины.

Дело в том, что в теории Ньютона предполагается, что гравитация окутывает всю вселенную и действует мгновенно в каждой её части. Однако, это невозможно исходя из того, что пределом допустимой скорости в физике является скорость света. Даже если бы скорость распространения гравитации была равна скорости света, она бы не могла мгновенно срабатывать даже на небольших участках космоса, поскольку нуждается в преодолении расстояния.

Решение проблемы нашлось в общей теории относительности Эйнштейна, которая рассматривает гравитацию не как силу, но как искривление времени-пространства под влиянием масс.

Для наглядности можно представить натянутую вокруг обруча ткань. После того, как на нее положат яблоко, она искривится. Если же после этого положить рядом тяжелую гирю, она искривится уже с центром в новом месте , а яблоко притянет к гире.

В физике элементарных частиц была выработана концепция гравитона — гипотетически существующей фундаментальной частицы, которая ответственна за гравитацию. Такая частица имеет нулевую массу, однако, обладает энергией, позволяющей ей влиять на поведение других элементарных частиц.

Понятие гравитационных волн

Несмотря на то, что общая теория относительности Эйнштейна уже давно была принята научным сообществом, она нашла очередное свое подтверждение с открытием физиками гравитационных волн в 2015 году.

Людям, далеким от теоретической физики и астрономии, будет нетрудно представить гравитационные волны в виде кругов, некоторое время разрастающихся, а затем затухающих после того, как в воду был брошен камень. Они имеют относительно похожую форму и структуру, но проявляются не на поверхности воды, а в пространстве-времени Вселенной.

Гравитационные волны оказывают дополнительное влияние на все близлежащие объекты и возникают при резкой смене массы в конкретной точке. Примером такого изменения в структуре космоса может быть слияние сверхмассивных черных дыр.

Ученые не могли столь долго открыть такие волны из-за низкой силы гравитации. Даже при сегодняшнем уровне развития технологий для этого пришлось поместить в вакуум четырехкилометровый детектор , состоящий из подвешенных зеркал.

Людям ошибочно кажется, что гравитация невероятно сильна. На самом же деле, это самая слабая из всех фундаментальных взаимодействий. Иллюстрацией того, насколько сильно её превосходит, к примеру, электромагнитное взаимодействие может служить факт того, что даже маленькие магниты на холодильник надежно закреплены магнитным притяжением на своем месте и будто игнорируют силу земного притяжения.

Выводы

Все тела во Вселенной взаимно притягиваются, это явление называется гравитацией. Сила притяжения, которая действует между двумя объектами, тем больше, чем больше их массы, в то же время тяготение уменьшается с увеличением расстояния.

После прочтения данной статьи ответ на вопрос, как формулируется закон всемирного тяготения, обязательно будет быстрым и правильным

Однако важно не забывать, что формула, описанная Ньютоном, справедлива только для конкретно описанных случаев

Более того, несмотря на существование и подтверждение новых гипотез, ньютоновская механика, включая закон всемирного тяготения, является наиболее простой из существующих теорий и верно описывает природные явления в своих границах.